

  
|
 |

ФУНКЦИЙ ТЕОРИЯ,
раздел математики, занимающийся изучением свойств различных функций. Теория функций распадается на две области: теорию функций действительного переменного и теорию функций комплексного переменного, различие между которыми настолько велико, что обычно их рассматривают порознь. Не вдаваясь в детали, можно сказать, что по существу речь идет о различии, с одной стороны, в детальном изучении основных понятий математического анализа (таких, как непрерывность, дифференцирование, интегрирование и т.п.), а с другой стороны, в теоретическом развитии анализа конкретных функций, представимых степенными рядами. Одним из достижений теории функций действительного переменного стало создание хорошей теории интегрирования, которую мы рассмотрим ниже. См. также АНАЛИЗ В МАТЕМАТИКЕ;
МАТЕМАТИЧЕСКИЙ АНАЛИЗ;
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ;
ФУНКЦИЯ;
ЧИСЛО;
РЯДЫ;
МНОЖЕСТВ ТЕОРИЯ;
ТОПОЛОГИЯ.
ФУНКЦИИ ДЕЙСТВИТЕЛЬНОГО ПЕРЕМЕННОГО
Функции, используемые в элементарном анализе, задаются формулами. Их графики обычно можно начертить, не отрывая карандаш от бумаги, как, например, график функции y = sinx, или они состоят из отдельных кусков, обладающих этим свойством, как, например, график функции y = tgx (рис. 1). Первоначально, когда строгое определение непрерывности отсутствовало, все функции, графики которых состоят из одного куска, считались обязательно непрерывными. Например, считалось, что непрерывной можно считать функцию, график которой не может лежать по обе стороны от прямой, не пересекая ее. Иначе говоря, непрерывная функция, принимая какие-либо два значения, непременно принимает и все промежуточные значения. Однако нетрудно найти функции, которые, хотя и заданы формулами и обладают указанным свойством, ведут себя не как непрерывные. Например, функция f(x) = sin(1/x) при x № 0 и f(0) = 0 (рис. 2) обладает свойством, о котором идет речь, однако, по мнению многих, не является непрерывной. Можно построить еще более удивительные примеры функций, принимающих действительное значение на любом сколь угодно малом интервале, но тем не менее не являющихся непрерывными. Графики таких функций не только невозможно начертить, но иногда даже и четко представить себе. С другой стороны, работы Ж.Фурье (1768–1830) и П.Дирихле (1805–1859), связанные с рядами Фурье показали, что некоторые заведомо разрывные функции задаются формулами, по крайней мере, если в число последних включить бесконечные ряды.
 (7.52 Кб) (7.52 Кб)
 (10.14 Кб) (10.14 Кб)
Возникшие при этом логические трудности были постепенно преодолены с помощью приема, типичного для теории функций: понятиям «функция» и «непрерывность» были даны строгие определения и исследованы вытекающие из них логические следствия. Оказалось, что эти следствия не находятся в точном соответствии с интуицией, о чем свидетельствуют приведенные примеры. Один из самых знаменитых примеров такого рода был предложен К .Вейерштрассом (1815–1897) – пример непрерывной, но нигде (ни в одной точке) не дифференцируемой функции. У математика, столкнувшегося с таким примером, может возникнуть много вопросов, например, «У каких непрерывных функций существуют производные?», или «Как можно изменить понятие производной, чтобы оно стало применимым к большинству непрерывных функций?», или «Какими дополнительными свойствами обладают недифференцируемые функции?». Проблемами такого рода и занимается теория функций действительного переменного.
Первое, что требуется от теории функций, – дать определение понятия «функции». Мы не станем приводить здесь самое общее из возможных определений, а просто скажем, что функция – это правило, которое каждому числу (или каждой точке) из данного множества ставит в соответствие другое число, называемое значением функции в этой точке. (См. ФУНКЦИЯ.)
Например, одна функция ставит в соответствие каждому действительному числу его квадрат, другая ставит в соответствие каждому положительному действительному числу его логарифм, третья функция ставит в соответствие каждому рациональному числу, записанному в виде несократимой дроби, знаменатель этой дроби. Все названные функции имеют различные области определения; областью определения функции называется множество точек, на котором она определена.
Функция называется непрерывной в точке, если любому бесконечно малому приращению аргумента в этой точке соответствует бесконечно малое приращение функции. Функция, непрерывная во всех точках области определения, называется непрерывной. Например, функция, принимающая в точке x значение x2, непрерывна; но функция, принимающая в точке x значение, равное ближайшему к x целому числу, не превосходящему x, непрерывной не является. В самом деле, значение этой функции изменяется скачком с 0 на 1, когда x изменяется от значения, меньшего 1/2 на сколь угодно малую величину, до значения, большего 1/2, на сколь угодно малую величину. На формальном математическом языке можно сказать, что функция f, принимающая значения f(x), непрерывна в точке y в том случае, если для любого положительного числа e найдется такое число d, что для всех точек x из области определения f(x), удовлетворяющих условию |x – y| < d, выполняется неравенство |f(x) – f(y)| < e.
Можно показать, что непрерывные функции, областями определения которых являются подмножества множества действительных чисел, обладают многочисленными свойствами, некоторые из которых интуитивно очевидны, а некоторые – нет. Например, сумма или произведение непрерывных функций также непрерывны. Если непрерывная функция в некоторой точке положительна, то всегда найдется достаточно малая ее окрестность, в которой она останется положительной. Если непрерывная функция принимает в двух точках различные значения a и b, то в промежуточных точках она принимает все значения, заключенные между a и b. Из последнего свойства можно заключить, например, что если растянутой резинке дать сжаться таким образом, чтобы она оставалась прямолинейной (не провисала), то одна из точек на ней останется неподвижной.
Функции, с которыми приходится иметь дело в математическом анализе, как правило, всюду непрерывны в области их определения, за исключением, быть может, отдельных изолированных точек. В то же время было построено много примеров разных функций как разрывных, так и нет, обладающих свойствами, противоречащими интуиции.
Хотя сумма двух непрерывных функций непрерывна, а следовательно, непрерывна и сумма любого конечного числа непрерывных функций, аналогичное утверждение для бесконечных сумм неверно. Например, бесконечная сумма
 является периодической (с периодом 2p) разрывной функцией, принимающей значения 0 при x = 0 и (1/2)(p – x) в интервале от 0 до 2p (рис. 3). Для того, чтобы ряд из непрерывных функций обязательно имел непрерывную сумму, необходимы более сильные условия, чем сходимость в каждой точке общей области определения функций. С другой стороны, предел непрерывных функций или повторный предел имеет все основания считаться формулой, и один из разделов теории функций занимается проблемой выяснения, какого рода функции представимы такими формулами. Согласно классификации разрывных функций, предложенной Р.Бэром (около 1899) непрерывные функции принадлежат 0-му классу, пределы непрерывных функций принадлежат 1-му классу и т.д. Функция, график которой изображен на рис. 3, принадлежит 1-му классу; функция
является периодической (с периодом 2p) разрывной функцией, принимающей значения 0 при x = 0 и (1/2)(p – x) в интервале от 0 до 2p (рис. 3). Для того, чтобы ряд из непрерывных функций обязательно имел непрерывную сумму, необходимы более сильные условия, чем сходимость в каждой точке общей области определения функций. С другой стороны, предел непрерывных функций или повторный предел имеет все основания считаться формулой, и один из разделов теории функций занимается проблемой выяснения, какого рода функции представимы такими формулами. Согласно классификации разрывных функций, предложенной Р.Бэром (около 1899) непрерывные функции принадлежат 0-му классу, пределы непрерывных функций принадлежат 1-му классу и т.д. Функция, график которой изображен на рис. 3, принадлежит 1-му классу; функция
 (3.92 Кб) (3.92 Кб)
 принимающая значения 1 при рациональных x и 0 при иррациональных x, принадлежит 2-му классу. Существуют функции, принадлежащие классу сколь угодно большого порядка, а также функции, вообще не принадлежащие какому-либо классу Бэра.
Были построены примеры, показывающие, что непрерывная функция необязательно должна иметь производную в каждой точке. У.Дини в 1877 предложил новое определение производной, применимое к любой функции и позволяющее заменить обычную производную во многих приложениях. Анализ функций с помощью различных обобщений производных позволил обнаружить многие свойства разрывных функций и показал, что большинство функций общего вида обладают внутренней симметрией.
принимающая значения 1 при рациональных x и 0 при иррациональных x, принадлежит 2-му классу. Существуют функции, принадлежащие классу сколь угодно большого порядка, а также функции, вообще не принадлежащие какому-либо классу Бэра.
Были построены примеры, показывающие, что непрерывная функция необязательно должна иметь производную в каждой точке. У.Дини в 1877 предложил новое определение производной, применимое к любой функции и позволяющее заменить обычную производную во многих приложениях. Анализ функций с помощью различных обобщений производных позволил обнаружить многие свойства разрывных функций и показал, что большинство функций общего вида обладают внутренней симметрией.
Одним из важных классов функций являются так называемые монотонные функции, т.е. либо возрастающие, либо убывающие. (Возрастающей называется функция, которая б 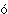 льшим значениям переменной из области определения ставит в соответствие б льшим значениям переменной из области определения ставит в соответствие б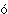 льшие значения функции.) Разность двух возрастающих функций обладает свойством, известным под названием «ограниченная вариация», что означает, что график такой разности не может совершать слишком сильные колебания; каждая функция ограниченной вариации записывается в виде разности двух монотонных функций. Лишь те функции, которые «сшиты» из конечного числа монотонных функций, могут быть достаточно убедительно представлены в графическом виде. Наконец, монотонная функция почти всюду дифференцируема. льшие значения функции.) Разность двух возрастающих функций обладает свойством, известным под названием «ограниченная вариация», что означает, что график такой разности не может совершать слишком сильные колебания; каждая функция ограниченной вариации записывается в виде разности двух монотонных функций. Лишь те функции, которые «сшиты» из конечного числа монотонных функций, могут быть достаточно убедительно представлены в графическом виде. Наконец, монотонная функция почти всюду дифференцируема.
Словам «почти всюду» можно придать точный смысл, который восходит к теории интегрирования, но можно это сделать и независимо от теории. Множество действительных чисел называется множеством меры нуль, если его можно покрыть счетным семейством интервалов сколь угодно малой суммарной длины. Например, множество рациональных чисел имеет меру нуль, так как оно счетно: при любом сколь угодно малом числе e мы можем покрыть первое рациональное число интервалом длиной e/2, второе число – интервалом длиной e/4, третье – интервалом длиной e/8 и т.д.; в результате все множество окажется покрыто интервалами (частично пересекающимися), суммарная длина которых составляет e(1/2 + 1/4 + 1/8 + ...) = e. Множество точек, в которых монотонная функция не имеет производной, является множеством меры нуль. В теории функций имеется много теорем, утверждающих, что некоторая функция обладает каким-либо свойством всюду, кроме множества меры нуль или множества, «малого» в том или ином смысле.
Хотя не все непрерывные функции дифференцируемы, многие дифференцируемые функции встречаются на практике, и все дифференцируемые функции непрерывны. В качестве примера свойств дифференцируемых функций приведем теорему Ролля, которая утверждает, что если действительная функция непрерывна на некотором отрезке, имеет в каждой его точке производную, а на концах принимает равные значения, то на этом интервале существует хотя бы одна точка, в которой производная этой функции равна нулю. Геометрический смысл этой теоремы состоит в том, что на графике такой функции существует такая точка, принадлежащая заданному интервалу, что в ней касательная к графику параллельна оси x. Отсюда нетрудно вывести так называемую теорему о среднем: если функция f непрерывна и дифференцируема на отрезке и a и b – две точки, принадлежащие этому отрезку, то
f (b) – f (a) = (b – a)f ў (c),
где c – некоторая точка между a и b.
Другим важным свойством действительной функции является выпуклость. Говорят, что функция выпукла вниз, если дуга ее графика, заключенная между любыми двумя точками, лежит ниже соединяющей их хорды (рис. 4). Можно показать, что функция выпукла вниз, если для любого интервала, стягивающая его хорда, находится выше кривой. Выпуклая вниз функция дифференцируема всюду, кроме, быть может, счетного числа «изломов», а ее производная сама является возрастающей функцией.
 (9.11 Кб) (9.11 Кб)
Еще одним типичным примером задач теории функций действительного переменного может служить задача аппроксимации данной функции функциями определенного рода. Если аппроксимирующие функции – суммы синусов или косинусов, то это центральная задача гармонического анализа; на практике здесь часто имеется ввиду представление данного колебания суммой гармоник. Задача приближения непрерывных функций многочленами возникает во многих практически важных областях, например, при проектировании механических устройств для вычерчивания (приближенного) графика заданной кривой или при создании быстродействующих компьютерных программ для вычисления значений сложных функций. Согласно доказанной Вейерштрассом в 1885 теореме о приближении функций, любую функцию, непрерывную на замкнутом интервале, можно сколь угодно точно аппроксимировать многочленами либо суммами синусов и косинусов. Слова «сколь угодно точно» здесь означают, что разность между данной функцией и функциями ее аппроксимирующими может быть сделана сколь угодно малой равномерно на всем интервале (если графики данной функции и аппроксимирующих функций начертить на бумаге, то при достаточно точной аппроксимации эти графики будут неотличимы).
Теория функций занимается также изучением свойств функций, размерности области определения которых более единицы (функции нескольких переменных). Отсюда уже можно перейти к функциям, областями определения которых служат разного рода абстрактные пространства, и даже к функциям, значения которых также принадлежат многомерным пространствам (таковы, например, векторные поля в физике) или абстрактным пространствам. Таким образом, теория функций незаметно переходит, с одной стороны, в функциональный анализ, а с другой – в топологию.
дальше
|
 |
 |



|


 (7.52 Кб)
(7.52 Кб) (10.14 Кб)
(10.14 Кб) является периодической (с периодом 2p) разрывной функцией, принимающей значения 0 при x = 0 и (1/2)(p – x) в интервале от 0 до 2p (рис. 3). Для того, чтобы ряд из непрерывных функций обязательно имел непрерывную сумму, необходимы более сильные условия, чем сходимость в каждой точке общей области определения функций. С другой стороны, предел непрерывных функций или повторный предел имеет все основания считаться формулой, и один из разделов теории функций занимается проблемой выяснения, какого рода функции представимы такими формулами. Согласно классификации разрывных функций, предложенной Р.Бэром (около 1899) непрерывные функции принадлежат 0-му классу, пределы непрерывных функций принадлежат 1-му классу и т.д. Функция, график которой изображен на рис. 3, принадлежит 1-му классу; функция
является периодической (с периодом 2p) разрывной функцией, принимающей значения 0 при x = 0 и (1/2)(p – x) в интервале от 0 до 2p (рис. 3). Для того, чтобы ряд из непрерывных функций обязательно имел непрерывную сумму, необходимы более сильные условия, чем сходимость в каждой точке общей области определения функций. С другой стороны, предел непрерывных функций или повторный предел имеет все основания считаться формулой, и один из разделов теории функций занимается проблемой выяснения, какого рода функции представимы такими формулами. Согласно классификации разрывных функций, предложенной Р.Бэром (около 1899) непрерывные функции принадлежат 0-му классу, пределы непрерывных функций принадлежат 1-му классу и т.д. Функция, график которой изображен на рис. 3, принадлежит 1-му классу; функция
 (3.92 Кб)
(3.92 Кб) принимающая значения 1 при рациональных x и 0 при иррациональных x, принадлежит 2-му классу. Существуют функции, принадлежащие классу сколь угодно большого порядка, а также функции, вообще не принадлежащие какому-либо классу Бэра.
Были построены примеры, показывающие, что непрерывная функция необязательно должна иметь производную в каждой точке. У.Дини в 1877 предложил новое определение производной, применимое к любой функции и позволяющее заменить обычную производную во многих приложениях. Анализ функций с помощью различных обобщений производных позволил обнаружить многие свойства разрывных функций и показал, что большинство функций общего вида обладают внутренней симметрией.
принимающая значения 1 при рациональных x и 0 при иррациональных x, принадлежит 2-му классу. Существуют функции, принадлежащие классу сколь угодно большого порядка, а также функции, вообще не принадлежащие какому-либо классу Бэра.
Были построены примеры, показывающие, что непрерывная функция необязательно должна иметь производную в каждой точке. У.Дини в 1877 предложил новое определение производной, применимое к любой функции и позволяющее заменить обычную производную во многих приложениях. Анализ функций с помощью различных обобщений производных позволил обнаружить многие свойства разрывных функций и показал, что большинство функций общего вида обладают внутренней симметрией.
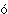 льшим значениям переменной из области определения ставит в соответствие б
льшим значениям переменной из области определения ставит в соответствие б (9.11 Кб)
(9.11 Кб)