

  
|
 |

Современная точка зрения.
У работы де Бройля, несмотря на ее достоинства, был один весьма серьезный недостаток. Традиционные теории света и вещества имели значительный успех потому, что в их основе лежали уравнения движения – особые системы дифференциальных уравнений, с помощью которых по состоянию в данный момент можно определить ее будущее состояние. Простые правила де Бройля не ведут непосредственно к таким уравнениям, равно как и умалчивают о том, какого рода волна обладает свойствами, определяемыми соотношениями (1) и (6). Уравнения движения были выведены почти одновременно Шрёдингером, работавшим над обобщением теории де Бройля, и Гейзенбергом, который совершенно независимо пытался придать всей квантовой механике более абстрактную форму, чтобы можно было сохранить существенные элементы и опустить все необоснованные экстраполяции нашего повседневного опыта в мир микроскопических явлений. Теории Гейзенберга и Шрёдингера, внешне очень различные, оказались лишь разными математическими способами выражения одних и тех же законов, дав возможность написать уравнения движения, из которых затем было выведено количественное подтверждение многих известных атомных явлений.
Следующим шагом в развитии квантовой механики стало осознание ее существенно статистического характера. Еще в 1924 Эйнштейн высказал предположение о том, что волны де Бройля могут быть в некотором смысле волнами вероятности. Через два года М.Борн, учитель и сотрудник Гейзенберга, нашел точное и общее аналитическое выражение этой мысли. Шрёдингер ввел греческую букву y (пси) для обозначения «волновой функции» – зависящей от координат и времени переменной, которая в определенных ситуациях носит простой колебательный характер, т.е. представляет собой волну, удовлетворяющую соотношениям (1) и (6). Функция y в общем случае комплекснозначная, и поэтому было трудно понять, каков ее физический смысл. Борн постулировал, что наблюдаемой величиной является не функция y, а величина |y|2, т.е. произведение функции на комплексно-сопряженную величину, а численное значение |y|2 в какой-либо точке пропорционально вероятности найти частицу в этой точке, если мы попытаемся там ее обнаружить.
Гипотеза Борна при всей ее простоте и, казалось бы, правильности поставила, однако, больше вопросов, чем помогла решить. Дело в том, что если теория не может дать определенного ответа, а вынуждена в некоторых случаях ограничиться указанием вероятности события, то создается впечатление, что она в каком-то смысле является всего лишь приближением к некоторой более фундаментальной теории, позволяющей делать точные предсказания. Но разве главная задача теоретической физики не заключается в создании такой теории?
В 1927 Гейзенберг дал совершенно неожиданный ответ на такую критику квантовой теории. Путем простых рассуждений, основанных на анализе некоторых особых экспериментальных ситуаций, он показал, что точные измерения не всегда возможны даже в принципе и что эта существенная неизбежная неопределенность точнейшим образом отражается в вероятностной структуре квантовой механики. Лучше понять, в чем здесь дело, позволяет конкретный пример, впервые приведенный Бором. Согласно квантовой механике, при одновременном указании положения и импульса частицы существует некоторая неопределенность, выражаемая формулой
 где Dр и Dх – неопределенности в импульсе р частицы и ее координате х, измеряемой в направлении движения. Бор проделал мысленный эксперимент по определению величин х и р с помощью микроскопа. Хорошо известно, что изображение в микроскопе неизбежно в какой-то мере расплывчато из-за дифракции света в линзах, а это приводит к неопределенности Dх в измеренном положении частицы. Однако эту неопределенность можно уменьшить, если использовать свет с меньшей длиной волны, поскольку тогда изображение становится более четким. Но возникает новая трудность: в силу соотношения (2) у кванта света с меньшей длиной волны больше импульс, и даже если измерению подлежит только один квант, сталкивающийся с частицей, то это столкновение вносит существенную неопределенность в импульс, коль скоро положение точно измерено. Вычисляя неопределенности, нетрудно убедиться в том, что они удовлетворяют неравенству (8), и, таким образом, чем точнее выполняется измерение одной величины, тем б
где Dр и Dх – неопределенности в импульсе р частицы и ее координате х, измеряемой в направлении движения. Бор проделал мысленный эксперимент по определению величин х и р с помощью микроскопа. Хорошо известно, что изображение в микроскопе неизбежно в какой-то мере расплывчато из-за дифракции света в линзах, а это приводит к неопределенности Dх в измеренном положении частицы. Однако эту неопределенность можно уменьшить, если использовать свет с меньшей длиной волны, поскольку тогда изображение становится более четким. Но возникает новая трудность: в силу соотношения (2) у кванта света с меньшей длиной волны больше импульс, и даже если измерению подлежит только один квант, сталкивающийся с частицей, то это столкновение вносит существенную неопределенность в импульс, коль скоро положение точно измерено. Вычисляя неопределенности, нетрудно убедиться в том, что они удовлетворяют неравенству (8), и, таким образом, чем точнее выполняется измерение одной величины, тем б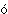 льшая неопределенность вносится в данные о другой.
Подкрепленное многими другими аналогичными рассуждениями, подтвержденное опытом и не имеющее ни одного «контрпримера», соотношение неопределенностей Гейзенберга представляет собой закон природы, который существует совершенно независимо от теории, способствовавшей его открытию. льшая неопределенность вносится в данные о другой.
Подкрепленное многими другими аналогичными рассуждениями, подтвержденное опытом и не имеющее ни одного «контрпримера», соотношение неопределенностей Гейзенберга представляет собой закон природы, который существует совершенно независимо от теории, способствовавшей его открытию.
Взгляды Гейзенберга и Бора на природу физического мира, открывшуюся в законах квантовой механики, привели к согласованной картине взаимоотношений теории и эксперимента, или, кратко говоря, физического содержания квантовой теории. Квантовая механика представляется теперь вполне корректной теорией, по крайней мере в круге явлений, к которым она должна применяться. Она выражена в весьма совершенной форме и сомнительно, чтобы ее самосогласованность была нарушена. Современная атомная теория революционизировала химические исследования, поскольку дала точную количественную интерпретацию по крайней мере наиболее простых химических фактов. Квантовая механика позволила также многое понять в биологических и даже генетических явлениях.
Квантовая механика заменяет атомную модель Резерфорда и Бора другой, на первый взгляд совершенно иной моделью, поскольку в нее существенным образом входит элемент вероятности. И действительно, квантовая механика (хотя она начинается с определенных и не содержащих никаких неоднозначностей уравнений) дает возможность вычислить относительную вероятность нахождения электрона в заданной точке пространства и с заданной скоростью или, точнее, в заданной малой области пространства со скоростью, лежащей в некотором диапазоне скоростей. В соответствии с теорией Бора и экспериментом электрон в атоме водорода в его основном состоянии с наибольшей вероятностью находится на расстоянии 10 –8 см от ядра, однако согласно квантовой механике и в отличие от теории Бора распределение вероятности его положения сферически симметрично в пространстве. В то же время имеется конечная вероятность обнаружить электрон вдали от ядра. Например, электрон может оказаться в километре от ядра, но вероятность найти его в малой области на таком расстоянии примерно в 101013 раз меньше, чем в такой же области с центром в ядре. На рис. 2,а показано распределение вероятности для электрона в атоме водорода, причем величина вероятности характеризуется плотностью ретуши на разрезе.
 (15.75 Кб) (15.75 Кб)
Допустим теперь, что в результате столкновения атому передается энергия. Электрон после столкновения будет двигаться по более удаленной от ядра орбите, и его пространственное вероятностное распределение изменится. Электрон может оказаться в различных возбужденных состояниях; он переходит в них, поглощая энергию. Через короткое время атом испустит квант света, электрон снова перейдет в основное состояние, и распределение вероятности примет прежний вид. Распределения на рис. 2, а и б характеризуются как бы «случайным» движением электрона, тогда как распределение, представленное на рис. 2,в, предполагает его движение по часовой стрелке, соответствующее орбитальному движению электрона в модели Бора. Изобразить столь же наглядно распределение вероятности в двухэлектронной системе невозможно, т.к. положения электронов статистически коррелированы (из-за взаимного отталкивания совместная вероятность нахождения электронов по разные стороны ядра больше, чем по одну и ту же его сторону); чтобы изобразить такое распределение, потребовалось бы каким-то образом построить шестимерное изображение – по три измерения на каждую частицу.
Сравнивая рис. 2 с боровскими эллиптическими орбитами, на первый взгляд не так-то просто усмотреть какую-либо связь между этими двумя моделями; поэтому трудно понять, почему теория Бора вообще имеет какое-то отношение к действительности. В определенном смысле она и в самом деле не адекватна действительности, чем и объясняется, что она иногда дает явно неверные ответы на некоторые вопросы. В то же время распределение вероятности на рис. 2, в обладает вполне узнаваемым сходством с боровской орбитой, а математический анализ динамики двух моделей обнаруживает глубокое соответствие между ними в некоторых важных пунктах. Например, было установлено, что движение, иллюстрируемое на рис. 2, соответствует вполне определенным, а не случайно распределенным значениям момента импульса. Эти значения даются соотношением (7) Бора – де Бройля с тем изменением, что теперь n может принимать нулевое значение. На рис. 2,а изображено состояние, которое вообще не обладает моментом импульса. Это совершенно невозможно ни в картине Резерфорда – Бора (поскольку электрон в таком случае должен был бы упасть на ядро), ни в картине де Бройля, поскольку тогда вообще не было бы никакой волны. Значения энергии для рассматриваемых случае также совершенно определенные и совпадают с теми, которые дают теория Бора и (с небольшими поправками, учитывающими слабые эффекты) эксперимент. Вследствие такого динамического соответствия между теорией Бора и квантовой теорией терминология, а отчасти даже мысленная картина, отвечающие модели Бора, по сей день в ходу у физиков, хотя для расчета атомных свойств и процессов, как правило, необходима квантовая механика.
Под «атомной теорией» часто понимают вычисления тех атомных и молекулярных характеристик, которые определяются электронами, движущимися вокруг тяжелых ядер. Дело в том, что благодаря хорошей экранировке ядра слоями электронов почти все его свойства практически не сказываются на поведении атома и их можно изучить отдельно. В этом смысле термин «атомная бомба» следует признать неудачным. Здесь уместнее было бы говорить о ядерной бомбе. При указанном же выше понимании термина «атомный» можно сказать, что перед современной атомной теорией стоят проблемы и трудности преимущественно вычислительного характера. Эта теория говорит нам, какие уравнения необходимо решить, но при анализе структуры сложного атома эти уравнения становятся столь сложными, что для их решения приходится прибегать к помощи компьютеров.
В строении атомного ядра все еще остается много неясного, хотя, по-видимому, квантовомеханический подход и здесь позволит справиться с имеющимися трудностями. Было бы, наверное, преувеличением утверждать, что современная атомная и ядерная теория обрели свою окончательную форму. Неясность в отношении многих проблем физики элементарных частиц учит нас величайшей осторожности в этом отношении. И все же тот огромный объем экспериментальных данных, относящихся к неядерным свойствам атомов, которые успешно объясняет современная теория, и отсутствие убедительных противоречащих ей экспериментов свидетельствуют (насколько можно судить) о том, что оставшиеся загадки атомной физики связаны с ядром и входящими в состав атома элементарными частицами; что же касается общей структуры атома, то наше понимание ее, видимо, следует считать достаточно полным. См. также АТОМНОГО ЯДРА СТРОЕНИЕ.
Наконец, стоит бросить ретроспективный взгляд на ранние атомистические учения с тем, чтобы посмотреть, какие из основных идей этих учений выжили. Роль атомов в учении Демокрита сейчас играют молекулы, т.е. устойчивые группы атомов, являющиеся мельчайшими частицами химических соединений. В этом смысле, как и утверждал Демокрит, все материальные вещества состоят из атомов. Демокрит умалчивал, почему атомы и молекулы обладают той формой и теми свойствами, которые им присущи. Но он ничего не знал о механике, науке, которая говорит, как движутся тела под действием сил. Он и представить себе не мог дифференциальные уравнения, решениями которых определяются свойства атомов и молекул, но, даже бросив беглый взгляд на рис. 2, можно понять, что эти решения, наглядно представленные на рисунке для простейшего случая, в действительности не что иное, как геометрические формы. Следовательно, атом и молекула «оказываются» не частицами вещества, а решениями уравнений, и догадка Платона представляется вполне оправданной, но как предвосхищение физики 20 в., а не окончательной теории строения материи (ибо кто может поручиться, что такая теория когда-нибудь будет построена).
Разумеется, атомы и молекулы, о которых мы говорили в этой статье, это не то, что имели в виду древнегреческие мыслители. Греческие философы говорили о мельчайших частичках материи, которые мы назвали бы элементарными частицами. Теория элементарных частиц в настоящее время еще весьма фрагментарна, но пронизана представлениями квантовой механики (что может быть как сильной, так и слабой ее стороной), так что сказанное выше о гипотезе Платона применимо в этом случае. Кроме того, мы знаем очень простое решение старой загадки: что произойдет, если попытаться разрезать то, что не разрезается? Ключом к разгадке служит открытая Эйнштейном эквивалентность массы и энергии, воплощенная в знаменитом соотношении E = mc2. Чтобы что-нибудь разрезать, нужно затратить энергию. Физики обходятся без ножей при исследовании свойств частиц, подвергая их бомбардировке другими частицами высоких энергий. Энергия может превращаться в массу при столкновении. Поэтому после столкновения может образоваться больше частиц, и не обязательно более легких, чем исходные, – нередко новые частицы обладают большей массой. Но это отнюдь не означает, что ни одну из частиц, называемых ныне элементарными, никогда не удастся расщепить; можно было бы думать, что для их расщепления потребуются новые методы и частицы-«снаряды» недостижимых пока энергий. См. также ЧАСТИЦЫ ЭЛЕМЕНТАРНЫЕ.
Находит свой отзвук в современной теории атома и индийское учение о первичности человеческого сознания и вторичности материального мира. Мы уже упоминали о том, что квантовая механика – теория существенным образом не детерминистская, а вероятностная. Можно дать абстрактное и вполне строгое математическое определение вероятности, но на практике в этом нет необходимости. Вероятность выигрыша на ипподроме во многом зависит от того, что вы видите в ходе заезда и какой информацией располагаете. Любое имеющее практическую ценность утверждение о вероятности относится к миру, каким его знает некое лицо или некая группа лиц. Наиболее важные и типичные заключения атомной теории имеют вид утверждений не о том, каков есть мир, а о том, каким он представится наблюдателю, располагающему определенными средствами наблюдения и определенной суммой ранее накопленных знаний. Современные физики и философы не думают, что квантовая механика – окончательная форма физической теории; ведется немало споров о том, как лучше перевести ее математические выражения в непротиворечивую картину мира, но все же трудно поверить, что резкое разграничение между внутренним и внешним, между «я» и «другим» с предельной ясностью выраженное Р.Декартом, но почти с самого начала присущее западной философии, сохранится в физике на самом фундаментальном ее уровне.
назад
|
 |
 |



|


 где Dр и Dх – неопределенности в импульсе р частицы и ее координате х, измеряемой в направлении движения. Бор проделал мысленный эксперимент по определению величин х и р с помощью микроскопа. Хорошо известно, что изображение в микроскопе неизбежно в какой-то мере расплывчато из-за дифракции света в линзах, а это приводит к неопределенности Dх в измеренном положении частицы. Однако эту неопределенность можно уменьшить, если использовать свет с меньшей длиной волны, поскольку тогда изображение становится более четким. Но возникает новая трудность: в силу соотношения (2) у кванта света с меньшей длиной волны больше импульс, и даже если измерению подлежит только один квант, сталкивающийся с частицей, то это столкновение вносит существенную неопределенность в импульс, коль скоро положение точно измерено. Вычисляя неопределенности, нетрудно убедиться в том, что они удовлетворяют неравенству (8), и, таким образом, чем точнее выполняется измерение одной величины, тем б
где Dр и Dх – неопределенности в импульсе р частицы и ее координате х, измеряемой в направлении движения. Бор проделал мысленный эксперимент по определению величин х и р с помощью микроскопа. Хорошо известно, что изображение в микроскопе неизбежно в какой-то мере расплывчато из-за дифракции света в линзах, а это приводит к неопределенности Dх в измеренном положении частицы. Однако эту неопределенность можно уменьшить, если использовать свет с меньшей длиной волны, поскольку тогда изображение становится более четким. Но возникает новая трудность: в силу соотношения (2) у кванта света с меньшей длиной волны больше импульс, и даже если измерению подлежит только один квант, сталкивающийся с частицей, то это столкновение вносит существенную неопределенность в импульс, коль скоро положение точно измерено. Вычисляя неопределенности, нетрудно убедиться в том, что они удовлетворяют неравенству (8), и, таким образом, чем точнее выполняется измерение одной величины, тем б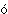 льшая неопределенность вносится в данные о другой.
Подкрепленное многими другими аналогичными рассуждениями, подтвержденное опытом и не имеющее ни одного «контрпримера», соотношение неопределенностей Гейзенберга представляет собой закон природы, который существует совершенно независимо от теории, способствовавшей его открытию.
льшая неопределенность вносится в данные о другой.
Подкрепленное многими другими аналогичными рассуждениями, подтвержденное опытом и не имеющее ни одного «контрпримера», соотношение неопределенностей Гейзенберга представляет собой закон природы, который существует совершенно независимо от теории, способствовавшей его открытию.
 (15.75 Кб)
(15.75 Кб)